Η Θεωρία της Ειδικής Σχετικότητας και η Διαστολή του Χρόνου

Εισαγωγή

Το 1905, ο Albert Einstein διατύπωσε μια Θεωρία που θα μετέβαλλε εντελώς την αντίληψή μας για τον χώρο και τον χρόνο. Ο Einstein Θεμελίωσε την ειδική Θεωρία της σχετικότητας διατυπώνοντας την εξής γενική υπόθεση, η οποία σήμερα είναι γνωστή ως Αρχή της Σχετικότητας:

Όλοι οι νόμοι της φυσικής είναι ίδιοι σε
όλα τα αδρανειακά συστήματα αναφοράς.

Σύμφωνα με τα γραφόμενα του ίδιου του Einstein, «....οι iδιοι νόμοι της ηλεκτροδυναμικής και της οπτικής ισχύουν σε όλα τα συστήματα αναφοράς στα οποία ισχύουν οι εξισώσεις της μηχανικής». Αυτή η απλή φράση εiναι μια γενίκευση της αρχής της σχετικότητας του Νεύτωνα και αποτελεi τη βάση της ειδικής Θεωρίας της σχετικότητας.

Μια δεύτερη υπόθεση που έκανε ο Eίnstein είναι η εξής:

Η ταχύτητα του φωτός στο κενό έχει την ίδια τιμή,
, σε όλα τα αδρανειακά συστήματα αναφοράς.

Με άλλα λόγια, οποιοσδήποτε μετρά την ταχύτητα του φωτός θα βρει την ίδια τιμή, c. Αν αποδεχθούμε τη Θεωρία της σχετικότητας του Einstein, πρέπει να συμπεράνουμε ότι η σχετική κίνηση δεν έχει καμιά σημασία για τη μέτρηση της ταχύτητας του φωτός. Ταυτόχρονα, πρέπει να αλλάξουμε τις κοινές συμβατικές πεποιθήσεις μας για τον χώρο και τον χρόνο και να είμαστε προετοιμασμένοι για ορισμένες μάλλον παράξενες συνέπειες.

Συνέπειες της Ειδικής Σχετικότητας

Σχεδόν καθένας που έχει ασχοληθεί ακόμη και επιφανειακά με τις θετικές επιστήμες αντιλαμβάνεται μερικές εντυπωσιακές προβλέψεις που απορρέουν από την αντιμετώπιση της σχετικής κίνησης από τον Einstein. Αν μελετήσει κανείς ορισμένες από τις συνέπειες της σχετικότητας, θα διαπιστώσει ότι αντιτίθενται στις βασικές ιδέες μας για τον χώρο και τον χρόνο. Θα περιορίσουμε τη μελέτη μας στην έννοια του του χρόνου και του ταυτοχρονισμού, οι οποίες είναι εντελώς διαφορετικές στη σχετικιστική μηχανική από ό,τι είναι στη νευτώνεια μηχανική. Ομοίως συμβαίνει και για το μήκος (το οποίο όμως δεν αποτελεί αντικείμενο μελέτης του παρόντος άρθρου). Παραδείγματος χάριν μερικές συνέπειες της σχετικότητας είναι ότι η απόσταση μεταξύ δύο σημείων και το χρονικό διάστημα μεταξύ δύο συμβάντων εξαρτώνται από το σύστημα αναφοράς στο οποίο μετρούνται. Αυτό σημαίνει ότι στη σχετικότητα δεν υπάρχει η έννοια του απόλυτου μήκους ή του απόλυτου χρόνου. Επίπλέον, συμβάντα που συντελούνται ταυτοχρόνως σε διαφορετικές θέσεις σε ένα σύστημα, δεν είναι, εν γένει, ταυτόχρονα σε ένα άλλο σύστημα.

Η σχετικότητα του ταυτοχρονισμού

Μια βασική παραδοχή της νευτώνειας μηχανικής είναι ότι υπάρχει μια παγκόσμια κλiμακα χρόνου η οποία είναι ίδια για όλους τους παρατηρητές. Πράγματι, ο Νεύτων έγραφε ότι «Ο απόλυτος, αληθινός και μαθηματικός χρόνος, από την ίδια του τη φύση, ρέει ομοιόμορφα χωρίς καμιά συσχέτιση με οτιδήποτε το εξωτερικό». Έτσι, ο Νεύτων και οι υποστηρικτές του θεώρησαν το ταυτόχρονο, απλώς, ως δεδομένο. Στην ειδική θεωρία της σχετικότητας, ο Einstein εγκατέλειψε αυτήν την υπόθεση. Σύμφωνα με τον Einstein, οι μετρήσεις, χρονικών διαστημάτων εξαρτώνται από το σύστημα αναφοράς στο οποίο γίνεται η μέτρηση.

Προκειμένου να επεξηγήσει το σημείο αυτό, ο Einstein επινόησε το εξής νοητικό πείραμα. 'Ενα όχημα κινείται με σταθερή ταχύτητα όταν δύο κεραυνοί χτυπούν τα άκρα του οχήματος, όπως δείχνει το Σχήμα 1α, αφήνοντας σημάδια στο όχημα και στο έδαφος. 'Εστωσαν Α' και Β' τα σημάδια που αποτυπώνονται στο όχημα και Α και Β τα αντίστοιχα σημάδια που αποτυπώνονται στο έδαφος. Ένας παρατηρητής στο σημείο Ο', ο οποίος κινείται με το όχημα, βρίσκεται στο μέσο της απόστασης μεταξύ των Α' και Β', ενώ ένας ακίνητος παρατηρητής στο σημείο Ο του εδάφους βρίσκεται στο μέσο της απόστασης μεταξύ των Α και Β. Τα συμβάντα που καταγράφονται από τους δύο παρατηρητές είναι τα φωτεινά σήματα που εκπέμπονται από τους κεραυνούς.

Ας υποθέσουμε ότι τα δύο φωτεινά σήματα φθάνουν στον ακίνητο παρατηρητή στο Ο την ίδια χρονική στιγμή, όπως φαίνεται στο Σχήμα 1β. Αυτός ο παρατηρητής αντιλαμβάνεται ότι τα φωτεινά σήματα έχουν διανύσει ίσες αποστάσεις με την ίδια ταχύτητα. Έτσι ο παρατηρητής στο σημείο Ο ορθά συμπεραίνει ότι τα συμβάντα στα σημεία Α και Β συντελούνται ταυτοχρόνως. Τώρα ας θεωρήσουμε τα ίδια συμβάντα, όπως τα αντιλαμβάνεται ο κινούμενος παρατηρητής στο σημείο Ο' του οχήματος. Τη χρονική στιγμή που τα φωτεινά σήματα φθάνουν στον ακίνητο παρατηρητή στο Ο, ο παρατηρητής στο Ο' έχει μετακινηθεί, όπως φαίνεται στο Σχήμα 1β. Συνεπώς, το φωτεινό σήμα από το Β' έχει ήδη αφιχθεί στο Ο', ενώ το φωτεινό σήμα από το Α' δεν έχει ακόμη φθάσει στο Ο'.

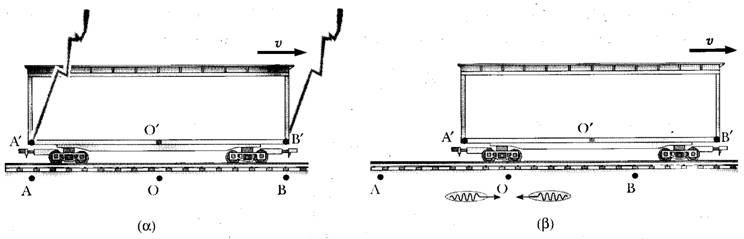
Σχήμα 1: Δύο κεραυνοί χτυπούν τα άκρα ενός κινούμενου οχήματος. (α) Τα συμβάντα φαίνονται ότι είναι ταυτόχρονα
για τον ακίνητο παρατηρητή στο Ο, ο οποίος βρίσκεται στο μέσο της απόστασης μεταξύ των Α και Β. (β) Τα συμβάντα
δεν φαίνονται ότι είναι ταυτόχρονα για τον κινούμενο παρατηρητή στο Ο', ο οποίος υποστηρίζει ότι το πρόσθιο άκρο
του οχήματος υφίσταται το χτύπημα του κεραυνού πριν από το οπίσθιο άκρο

Σύμφωνα με τον Einstein, o παρατηρητής στο O' πρέπει να παρατηρεί ότι το φως διαδίδεται με την ίδια ταχύτητα που μετρείται και από τον παρατηρητή στο O. Συνεπώς, o παρατηρητής στο O' συμπεραίνει ότι o κεραυνός χτυπά το πρόσθιο άκρο του οχήματος προτού χτυπήσει το οπίσθιο άκρο. Αυτό το ιδεατό πείραμα δείχνει σαφώς ότι τα δύο συμβάντα, τα οποία φαίνονται ότι είναι ταυτόχρονα για τον παρατηρητή στο O, δεν φαίνονται να είναι ταυτόχρονα για τον παρατηρητή στο Ο'. Με άλλα λόγια,

δύο συμβάντα τα οποία είναι ταυτόχρονα σε ένα σύστημα αναφοράς, δεν είναι,
εν γένει, ταυτόχρονα σε ένα δεύτερο σύστημα που κινείται ως προς το πρώτο.
Αυτό σημαίνει ότι o ταυτοχρονισμός δεν είναι απόλυτη έννοια.

Σ’ αυτό το σημείο, ίσως αναρωτηθείτε ποια από τις δύο παρατηρήσεις είναι σωστή σε ό,τι αφορά τα δύο συμβάντα. H απάντηση είναι ότι και οι δύο είναι σωστές, επειδή η Αρχή της Σχετικότητας αναφέρει ότι δεν υπάρχει κάποιο προνομιακό αδρανειακό σύστημα αναφοράς. Μολονότι οι δύο παρατηρητές καταλήγουν σε διαφορετικά συμπεράσματα, και οι δύο έχουν δίκιο στο δικό τους σύστημα αναφοράς, επειδή η έννοια του ταυτοχρονισμού δεν είναι απόλυτη. Πράγματι, αυτό είναι το κεντρικό σημείο της σχετικότητας – δηλαδή κάθε αδρανειακό σύστημα αναφοράς μπορεί να χρησιμοποιηθεί για την καταγραφή συμβάντων και τη μελέτη φυσικών φαινομένων. Δεν υπάρχει κάτι το λανθασμένο με τα ρολόγια ή με τα υποδεκάμετρα που χρησιμοποιούνται για την πραγματοποίηση των μετρήσεων. Απλώς τα χρονικά διαστήματα και οι μετρήσεις μήκους εξαρτώνται από τον παρατηρητή. Παρατηρητές σε διαφορετικά αδρανειακά συστήματα αναφοράς θα μετρούν διαφορετικά χρονικά διαστήματα με τα ρολόγια τους και διαφορετικές αποστάσεις με τα υποδεκάμετρά τους. Ωστόσο, και οι δύο Θα συμφωνούν σε ό,τι αφορά τους νόμους της φυσικής στα αντίστοιχα συστήματα αναφοράς τους, αφού οι νόμοι αυτοί είναι οι ίδιοι για όλους τους αδρανειακούς παρατηρητές. H σχετικότητα που διέπει τις μετρήσεις χρόνου και αποστάσεων δίνει τη δυνατότητα στους νόμους της φυσικής (συμπεριλαμβανομένων και των εξισώσεων του Maxwell) να είναι ίδιοι για όλους τους παρατηρητές που κινούνται με σταθερή ταχύτητα.

Διαστολή χρόνου

Προκειμένου να δείξουμε ότι o χρόνος δεν ρέει με τον ίδιο ρυθμό για δύο διαφορετικούς αδρανειακούς παρατηρητές, ας θεωρήσουμε ένα όχημα κινούμενο προς τα δεξιά με ταχύτητα u, όπως δείχνει το Σχήμα 2α. Στην οροφή του οχήματος είναι στερεωμένο ένα κάτοπτρο· και ένας παρατηρητής στο Ο', που βρίσκεται σε ακινησία ως προς το όχημα, κρατάει μια λυχνία φωτεινών παλμών σε απόσταση d από το κάτοπτρο. Σε κάποια στιγμή, η λυχνία εκπέμπει έναν φωτεινό παλμό. Επειδή o φωτεινός παλμός έχει ταχύτητα c, o χρόνος που απαιτείται ώστε o παλμός να μεταβεί από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία μπορεί να βρεθεί από τον ορισμό της ταχύτητας:

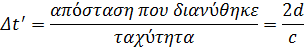
όπου η τονούμενη σημειογραφία δηλώνει ότι o χρόνος μετρήθηκε από τον παρατηρητή στο σύστημα αναφοράς του κινούμενου οχήματος.

Τώρα, ας εξετάσουμε το ίδιο σύνολο συμβάντων, όπως παρατηρούνται από έναν παρατηρητή που βρίσκεται στο σημείο O ενός ακίνητου συστήματος αναφοράς (Σχ. 2β). Σύμφωνα με τον παρατηρητή αυτόν, το κάτοπτρο και η λυχνία κινούνται προς τα δεξιά με ταχύτητα u. Τη στιγμή που το φως από τη λυχνία φθάνει στο κάτοπτρο, το κάτοπτρο θα έχει διανύσει μία απόσταση, όπου Δt είναι ο χρόνος που απαιτείται ώστε ο φωτεινός παλμός να μεταβεί από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία, όπως μετρείται από τον ακίνητο παρατηρητή που βρίσκεται στο Ο. Με άλλα λόγια, λόγω της κίνησης του συστήματος, ο ακίνητος παρατηρητής συμπεραίνει ότι, προκειμένου ο παλμός να προσπέσει στο κάτοπτρο πρέπει να φύγει από τη λυχνία υπό γωνία ως προς την κατακόρυφη διεύθυνση. Συγκρίνοντας τα Σχήματα 2α και 2β, βλέπουμε ότι το φως πρέπει να διανύσει μεγαλύτερη απόσταση στο ακίνητο σύστημα από ό,τι στο κινούμενο σύστημα.

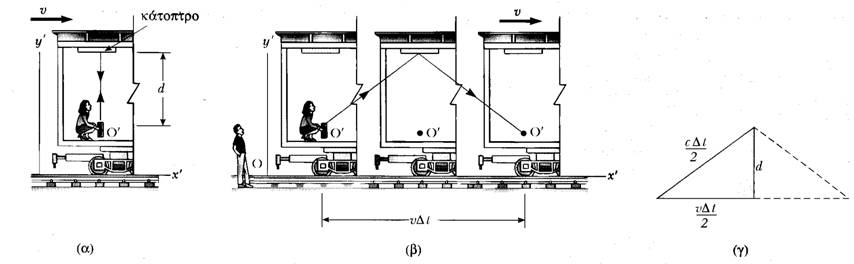
Σχήμα 2: (α) Ένα κάτοπτρο είναι στερεωμένο σε ένα κινούμενο όχημα και ένας φωτεινός παλμός εκπέμπεται από το σημείο Ο', το οποίο βρίσκεται
σε ηρεμία ως προς το όχημα. (β) Σε σχέση με τον ακίνητο παρατηρητή στο έδαφος, το κάτοπτρο και η πηγή παλμών Ο' κινούνται με ταχύτητα u.
Σημειώστε ότι η απόσταση που διανύει ο παλμός όπως αυτή μετρείται από τον ακίνητο παρατηρητή είναι μεγαλύτερη από 2d. (γ) Το ορθογώνιο
τρίγωνο για τον υπολογισμό της σχέσης μεταξύ Δt και Δt'

Τώρα, σύμφωνα με τον Einstein, η ταχύτητα του φωτός πρέπει να είναι c και για τους δύο παρατηρητές. Συνεπώς, προκύπτει ότι το χρονικό διάστημα Δt που μετρείται από έναν παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από το χρονικό διάστημα Δt' που μετρείται από έναν παρατηρητή στο κινούμενο σύστημα. Για να βρούμε τη σχέση μεταξύ των Δt και Δt', είναι βολικό να χρησιμοποιήσουμε το ορθογώνιο τρίγωνο του Σχήματος 2γ. Η εφαρμογή του πυθαγόρειου Θεωρήματος στο συγκεκριμένο τρίγωνο δίνει

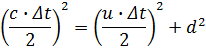
Λύνοντας ως προς Δt έχουμε:

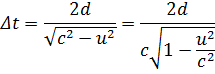
Επειδή είναι , μπορούμε να γράψουμε την προηγούμενη εξίσωση ως εξής

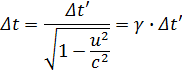
όπου 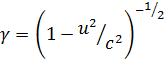. Το αποτέλεσμα αυτό δηλώνει ότι το χρονικό διάστημα που μετρείται από τον παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από εκείνο που μετρείται από τον παρατηρητή στο κινούμενο σύστημα (επειδή το γ είναι πάντοτε μεγαλύτερο από τη μονάδα).

Σύμφωνα με έναν ακίνητο παρατηρητή, ένα κινούμενο ρολόι είναι
πιο αργό κατά έναν συντελεστή από ένα ολόιδιο ακίνητο ρολόι.
Το φαινόμενο αυτό είναι γνωστό ως διαστολή του χρόνου.

Το χρονικό διάστημα Δt' ονομάζεται ιδιοχρόνος. Γενικά, ιδιοχρόνος ορίζεται το χρονικό διάστημα που μεσολαβεί μεταξύ δύο συμβάντων όταν η μέτρηση γίνεται από έναν παρατηρητή που βλέπει τα γεγονότα να συμβαίνουν στην ίδια θέση. Στην περίπτωσή μας, ο παρατηρητής στο Ο' μετράει τον ιδιοχρόνο. δηλαδή, ιδιοχρόνος είναι πάντοτε, ο χρόνος που μετρείται από έναν παρατηρητή ο οποίος κινείται μαζί με το ρολόι.

Είδαμε ότι τα κινούμενα ρολόγια «πάνε πιο αργά» κατά τον συντελεστή . Αυτό ισχύει και για τα συνήθη μηχανικά ρολόγια, καθώς και για το ρολόι «φωτός» που μόλις περιγράφηκε. Πράγματι, μπορούμε να γενικεύσουμε αυτά τα αποτελέσματα αναφέροντας ότι όλες οι φυσικές διεργασίες, συμπεριλαμβανομένων των χημικών αντιδράσεων και των βιολογικών διεργασιών, επιβραδύνονται σε, σχέση με ένα ακίνητο ρολόι όταν συμβαίνουν σε ένα κινούμενο σύστημα. Παραδείγματος χάριν, ο σφυγμός ενός αστροναύτη που κινείται στο Διάστημα θα πρέπει να προσαρμοστεί με την κλίμακα χρόνου ενός ρολογιού που βρίσκεται μέσα στο διαστημόπλοιο. Το ρολόι του αστροναύτη και ο σφυγμός του επιβραδύνονται σε σχέση με ένα ακίνητο ρολόι. Ο αστροναύτης όμως, προφανώς δεν αντιλαμβάνεται ότι ο ρυθμός ζωής επιβραδύνεται στο διαστημόπλοιο.

Η διαστολή του χρόνου είναι ένα πραγματικό φαινόμενο που έχει επιβεβαιωθεί με διάφορα πειράματα.

Αποσπάσματα από το βιβλίο: «Σύγχρονη Φυσική» - Κεφάλαιο 1^ο
των R.A.Serway – C.J.Moses – C.A.Moyer,
Πανεπιστημιακές Εκδόσεις Κρήτης 2001